和算を嗜む

模範回答

鶴と亀の足の本数の差は、$4 - 2 = 2$本である。

今、$100$ 匹全てが亀とすると、足の本数は、$4 × 100 = 400$本となる。

実際の足の本数は、$272$本なので、$400 - 272 = 128$本の差額が鶴の足の数となる。

よって、鶴は、$128 ÷ 2 = 64$ 羽と求められる。

ゆえに、亀は、$100 - 64 = 36$ 匹となる。

生成AIによる解法

答え：鶴 $64$ 羽、亀 $36$ 匹

模範回答

今、右に$13$列有り、下に、$13 + 1 = 14$個あると考えて、$13 × 14 ÷ 2 = 91$個あることとなる。

台形の面積と考える方法

上辺$1$、下辺$13$、高さ$13$の台形と考えて、面積を求めると、台形の面積の公式より、$( 1 + 13 ) × 13 ÷ 2 = 91$

生成AIによる解法

答え：$91$個

模範回答

$3ℓ$のコップを使って、$7ℓ$のコップが満杯になるまで入れると、$3 × 3 - 7 = 2ℓ$残る。$7ℓ$のコップを桶に戻して、$2ℓ$を入れて、もう一度、$3ℓ$のコップを入れれば、$2 + 3 = 5ℓ$となる。

生成AIによる解法

誤答

コップに移動させる過程で、何度も誤りを指摘したのですが、修正されることは無かったです。

模範回答

$4 × 4 = 16$個あり、下の碁石は必ず$12$個になるので、$16 + 12 = 28$個となる。

一次方程式による回答

この問題は、１辺が8個とあるが、この数は無くても正答が可能である。

１辺を$x$個あるとする。全体の個数は、$4(x - 1)$個とあろことになる。

並び替えると、$(3x + 4)$個あることが分かるので、

$4(x - 1) = 3x + 4$

これを解いて、$x = 8$

よって全体の個数は、$4(8 - 1) = 28$個と求められる。

模範回答

真ん中の正方形は、$a^2$。４隅の二等辺三角形は、全部で$a^2$。上下左右の長方形は、$a × \frac{a}{\sqrt{2}} × 4 = 2 \sqrt{2} a^2$。

全てを足すと、$a^2 + a^2 + 2 \sqrt{2} a^2 = 2 ( \sqrt{2} + 1 ) a^2$

生成AIによる解法

相似を使った回答

$9 : 12 = (9 + 12) : (12 + x)$

これを解いて、$x = 16$

青森県の三内丸山遺跡には、大型掘立柱建物跡がある。柱の直径は約1mで、柱穴の間隔、幅、深さがそれぞれ4.2m、2m、2mで全て一致する。日本では、縄文時代から測量技術が存在したことになる。

解法は、$999 × 999 × 999$ である。

その１

$(1000 - 1) × (1000 - 1)$

$= 1000000 - 2 × 1000 + 1$

$= 998001$

$998001 × (1000 - 1)$

$= 998001000 - 998001$

$= 997002999$

その２

$(1000 - 1)^3$

$=1000000000 - 3 × 1000^2 × 1 + 3 × 1000 × (-1)^2 -1$

$= 997002999$

生成AIによる解法

答え：$9$ 億 $9700$ 万 $2999$ 回

時は平安時代

口遊（くちずさみ）は、平安時代に源為憲（みなもとの　ためのり）により作成された。この資料の中には、$9 × 9 = 81$からなる九九表が掲載されている。平安時代には、九九が使われていたことが分かる。ただ、万葉集の和歌の中にも九九が登場することから、実際に、九九が伝わったのは、奈良時代と思われる。

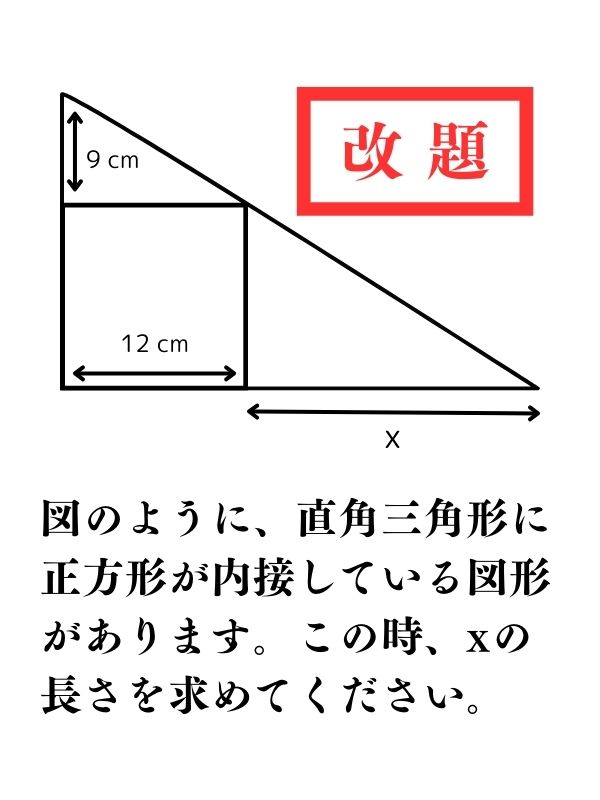
勾配

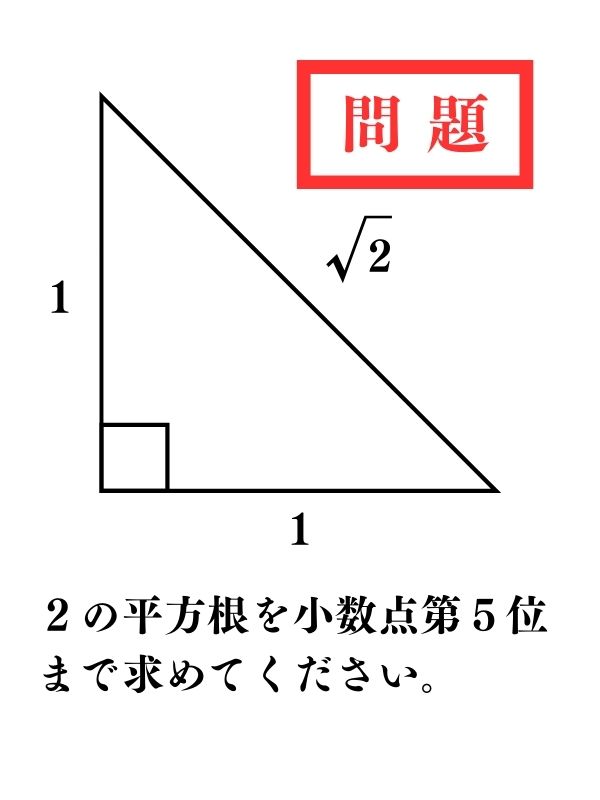
この時代は、図形において「角度」の概念が無かったようだ。その代わり、斜傾を１尺進むとどれだけ高くなるかという「勾配」を求めて計算していた。画像を見ると、$\sqrt{\smash[b]{2}} = 1.41421$と小数点第5位まで正確に計算されていることが分かります。

生成AIによる解法